1. 计算图
计算图将计算过程用图形表示出来。这里说的图形是数据结构图,通过多个节点和边表示(连接节点的直线称为“边”)。
正向传播(forward propagation):从左向右进行计算,传递的是计算结果。
反向传播(backward propagation):是从右向左进行计算,传递的是局部导数。
局部计算:计算图的特征是可以通过传递“局部计算”获得最终结果。“局部”这个词的意思是“与自己相关的某个小范围”。局部计算是指,无论全局发生了什么,都能只根据与自己相关的信息输出接下来的结果。
计算图的优点:
①可以进行局部计算。
②计算图可以将中间的计算结果全部保存起来。
③可以通过反向传播高效计算导数。
综上,计算图的优点是,可以通过正向传播和反向传播高效地计算各个变量的导数值。2. 链式法则

链式法则是关于复合函数的导数的性质,定义如下:
如果某个函数由复合函数表示,则该复合函数的导数可以用构成复合函数的各个函数的导数的乘积表示。
链式法则和计算图

最左边是反向传播的结果。
3. 反向传播
3.1 加法节点的反向传播

加法节点的反向传播只乘以1,所以输入的值会原封不动地流向下一个节点。
3.2 乘法节点的反向传播
考虑z=xy:

乘法的反向传播会将上游的值乘以正向传播时的输入信号的“翻转值”后传递给下游。翻转值表示一种翻转关系,如图所示,正向传播时信号是x的话,反向传播时则是y;正向传播时信号是y的话,反向传播时则是x。
加法的反向传播只是将上游的值传给下游,
并不需要正向传播的输入信号。但是,乘法的反向传播需要正向传播时的输入信号值。因此,实现乘法节点的反向传播时,要保存正向传播的输入信号。

4. 简单层的实现
我们把要实现的计算图的乘法节点称为“乘法层”(MulLayer),加法节点称为“加法层”(AddLayer)。
5. 激活函数层的实现
5.1 ReLU层
激活函数ReLU(Rectified Linear Unit)由下式表示:

求出y关于x的导数:
如果正向传播时的输入x大于0,则反向传播会将上游的值原封不动地传给下游。反过来,如果正向传播时的x小于等于0,则反向
传播中传给下游的信号将停在此处。
ReLU层的作用就像电路中的开关一样。正向传播时,有电流通过的话,就将开关设为 ON;没有电流通过的话,就将开关设为 OFF。
反向传播时,开关为ON的话,电流会直接通过;开关为OFF的话,则不会有电流通过。5.2 Sigmoid层
sigmoid函数式:


除了“×”和“+”节点外,还出现了新的“exp”和“/”节点。“exp”节点会进行y = exp(x)的计算,“/”节点会进行y=1/x的计算。
反向传播的流程:


反向传播的输出为 ,这个值会传播给下游的节点。
,这个值会传播给下游的节点。
因此,Sigmoid层的反向传播,只根据正向传播的输出就能计算出来:
6. Affine/Softmax层的实现
6.1 Affine层
- 神经网络的正向传播中,为了计算加权信号的总和,使用了矩阵的乘积运算。矩阵的乘积运算的要点是使对应维度的元素个数一致。
- 仿射变换:神经网络的正向传播中进行的矩阵的乘积运算在几何学领域被称为“仿射变换”。
- Affine层:将进行仿射变换的处理实现为“Affine层“。
几何中,仿射变换包括一次线性变换和一次平移,分别对应神经网络的加权和运算与加偏置运算。


6.2 批版本的Affine层
前面介绍的Affine层的输入X是以单个数据为对象的。现在我们考虑N个数据一起进行正向传播的情况,也就是批版本的Affine层。
6.3 Softmax-with-Loss 层

- 神经网络中进行的处理有推理(inference)和学习两个阶段。
神经网络的推理通常不使用 Softmax层。
神经网络的学习阶段则需要 Softmax层。 - 包含作为损失函数的交叉熵误差(cross entropy error),所以称为“Softmax-with-Loss层”。
- Softmax-with-Loss层的计算图:
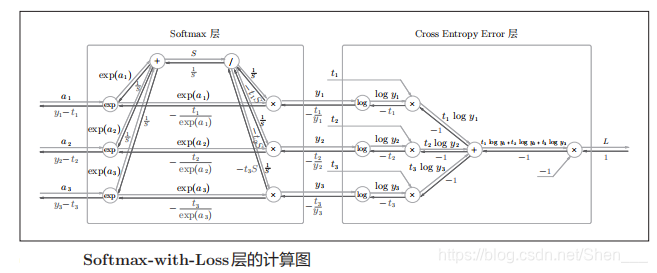
softmax函数记为Softmax层,交叉熵误差记为Cross Entropy Error层。这里假设要进行3类分类,从前面的层接收3个输入(得分)。如图5-30所示,Softmax层将输入(a1, a2, a3)正规化,输出(y1, y2,y3)。Cross Entropy Error层接收Softmax的输出(y1, y2, y3)和教师标签(t1, t2, t3),从这些数据中输出损失L。 - “简易版”的Softmax-with-Loss层的计算图:
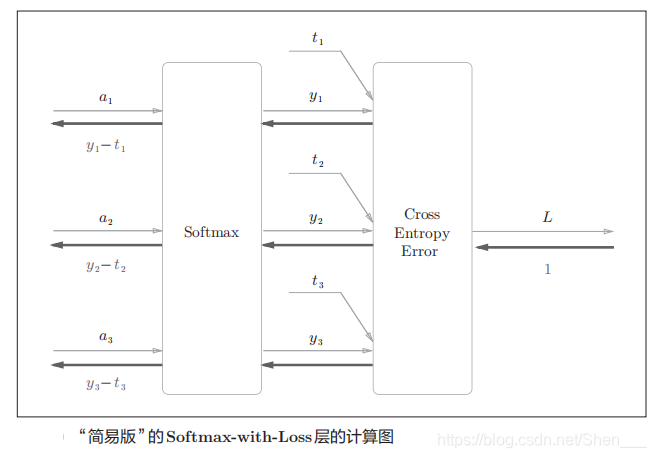
Softmax层的反向传播得到了(y1 − t1, y2 − t2, y3 − t3)这样“漂亮”的结果。由于(y1, y2, y3)是Softmax层的输出,(t1, t2, t3)是监督数据,所以(y1 − t1, y2 − t2, y3 − t3)是Softmax层的输出和教师标签的差分。神经网络的反向传播会把这个差分表示的误差传递给前面的层,这是神经网络学习中的重要性质。 - 神经网络学习的目的就是通过调整权重参数,使神经网络的输出(Softmax的输出)接近教师标签。
7. 误差反向传播法的实现
神经网络学习的步骤:
前提
神经网络中有合适的权重和偏置,调整权重和偏置以便拟合训练数据的
过程称为学习。神经网络的学习分为下面4个步骤。
步骤1(mini-batch)
从训练数据中随机选择一部分数据。
步骤2(计算梯度)
计算损失函数关于各个权重参数的梯度。
步骤3(更新参数)
将权重参数沿梯度方向进行微小的更新。
步骤4(重复)
重复步骤1、步骤2、步骤3。
计算梯度的两种方法:一种是基于数值微分的方法,另一种是解析性地求解数学式的方法。
数值微分虽然实现简单,但是计算要耗费较多的时间。和需要花费较多时间的数值微分不同,误差反向传播法可以快速高效地计算梯度。
数值微分的优点是实现简单,因此,一般情况下不太容易出错。而误差反向传播法的实现很复杂,容易出错。所以,经常会比较数值微分的结果和误差反向传播法的结果,以确认误差反向传播法的实现是否正确。确认数值微分求出的梯度结果和误差反向传播法求出的结果是否一致(严格地讲,是非常相近)的操作称为梯度确认(gradient check)。
小结
• 通过使用计算图,可以直观地把握计算过程
•计算图的节点是由局部计算构成的。局部计算构成全局计算。
•计算图的正向传播进行一般的计算。通过计算图的反向传播,可以计算各个节点的导数。
•通过将神经网络的组成元素实现为层,可以高效地计算梯度*(反向传播法)。
•通过比较数值微分和误差反向传播的结果,可以确认误差反向传播的实现是否正确(梯度确认)。
