概率图模型(probabilistic model)(变量关系图):是一类用图来表达变量相关关系的概率模型。
一个结点:表示一个或一组随机变量。
边:表示变量间的概率相关关系。
14.1 隐马尔科夫模型
- 概率模型:将学习任务归结于计算变量的概率分布。
- 推断:利用已知变量推测未知变量的条件分布。
- “生成式”模型:考虑联合概率分布P(Y,R|O)。
“判别式”模型:考虑条件分布P(Y|O)。
(Y:变量集合O:可观测变量集合 R:其他变量的集合) - 隐马尔科夫模型(Hidden Markov Model:简称HMM):是结构最简单的动态贝叶斯网,有向图模型,==生成式模型==。
- 隐马尔科夫模型中的变量:状态变量(隐变量)、观测变量。

- 状态(离散空间)空间:状态变量的取值范围。
- 马尔科夫链(Markov chain):系统下一时刻的状态仅有当前状态决定,不依赖于以往的任何状态。基于这种关系,所有变量的联合概率分布为:
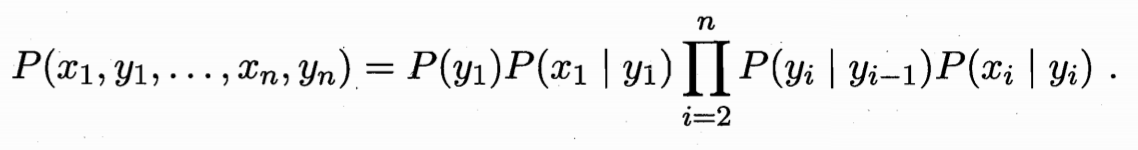
- 确定一个隐马尔科夫模型需要以下三组参数:
 )
)
- 产生观测序列的过程:

- 在实际应用中,人们常关注隐马尔科夫模型的三个基本问题:

14.2 马尔可夫随机场
- 马尔可夫随机场(Markov Random Field,简称MRF):是典型的马尔可夫网,无向图模型,==生成式模型==。
- 势函数(potential functions):亦称”因子“(factor),是定义在变量子集上的非负实函数,主要用于定义概率分布函数。

- 团(clique):对于上图中节点的一个子集,若其中任意两结点间都有边连接,则该结点子集为一个“团”。
- 极大团(maximal clique):在一个团中加入任何一个结点都不再形成团。不能被其他团所包含的团。
- 马尔可夫随机场中,多个变量之间的联合概率定义(基于团):
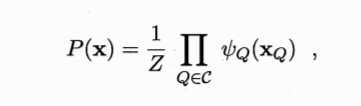
所有团构成的集合为C,团Q∈C。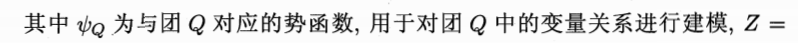 )
)
- 马尔可夫随机场中,多个变量之间的联合概率定义(基于极大团):
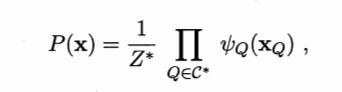

- 分离集(separating set):
 如图,从结点集A中的结点到B中的结点都必须经过结点集C中的结点,则称结点集A和B被结点集C分离,C成为“分离集”。
如图,从结点集A中的结点到B中的结点都必须经过结点集C中的结点,则称结点集A和B被结点集C分离,C成为“分离集”。 - 全局马尔可夫性(global Markov property):给定两个变量子集的分离集,则这两个变量子集条件独立。
- 由全局马尔可夫性得到的两个很有用的推论:
局部马尔可夫性(local Markov property):给定某变量的邻接变量,则该变量条件独立于其他变量。
成对马尔可夫性(pairwise Markov property):给定所有其他变量,两个非邻接变量条件独立。 - 马尔可夫随机场中的势函数:
作用:定量刻画变量集中变量之间的相关关系,它是非负函数,且在所偏好的变量取值上有较大函数值。
为了满足非负性,指数函数常被用于定义势函数:
14.3 条件随机场
- 条件随机场(Conditional Random Field,简称CRF):是一种==判别式==无向图模型。
- 条件随机场试图对多个变量在给定观测值后的条件概率进行建模。在自然语言处理的词性标注任务中,观测数据为语句(即单词序列),标记为相应的词性序列,具有线性序列结构;在语法分析任务中,输出标记则是语法树,具有树形结构。

- 条件随机场定义:

- 链式条件随机场(chain-structured CRF):

条件随机场使用势函数和图结构上的团来定义条件概率P(y|x)。
链式条件随机场主要包含两种关于标记变量的团:单个标记变量和相邻的标记变量。 - 在条件随机场中,通过选用指数势函数并引入特征函数,条件概率被定义为:

- 特征函数:特征函数通常是实值函数,以刻画数据的一些很可能成立或期望成立的经验特征。
例:14.5(a)的词性标注,若采用转移特征函数:
- 条件随机场和马尔可夫随机场均使用团上的势函数定义概率,两者在形式上没有显著差别;但条件随机场处理的是条件概率,而马尔科夫随机场处理的是联合概率。
14.4 学习与推断
边际分布:指对无关变量求和或积分后得到结果。
边际化:对联合分布中其他无关变量进行积分的过程。
参数估计(参数学习问题):对概率图模型,确定具体分布的参数。通常使用极大似然估计或最大后验概率估计求解。
推断问题的目标和关键:

概率图模型的推断方法大致可分为两类:
第一类:精确推断方法——变量消去、信念传播。
第二类:近似推断方法——MCMC采样、变分推断。14.4.1 变量消去
精确推断的实质是一类动态规划算法,它利用图模型所描述的条件独立行来削减计算目标概率值所需要的计算量。
有向图模型:
 )
) )
)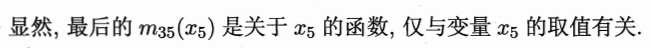
无向图模型:上述方法对无向图模型同样适用,忽略掉图14.7(a)中的箭头,将其看作一个无向图模型,有

变量消去法有一个明显的缺点:若需计算多个边际分布,重复使用变量消去法将会造成大量的冗余计算。
14.4.2 信念传播
信念传播(Belief Propagation)算法:将变量消去法中的求和操作看作一个消息传递过程,较好地解决了求解多个边际分布时的重复计算问题。
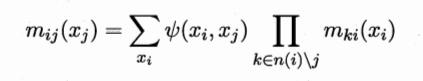

在信念传播算法中,一个结点仅在接收到来自其他所有结点的消息后才能向另一个结点发送消息,且结点的边际分布正比于它所接收的消息的乘积,即
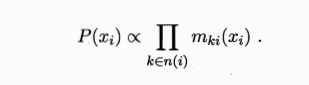
若图结构中没有环,则信念传播算法经过两个步骤即可完成所有消息传递,进而能计算所有变量上的边际分布:
●指定一个根结点,从所有叶结点开始向根结点传递消息,直到根结点收到
所有邻接结点的消息;
●从根结点开始向叶结点传递消息,直到所有叶结点均收到消息。
例:
14.5 近似推断
近似推断方法大致可分为两大类:
第一类:采样(sampling),通过使用随机化方法完成近似;
第二类:使用确定性近似完成近似推断,典型代表为变分推断(variational inference)。14.5.1 MCMC采样
采样思路:
假设我们的目标是计算函数f(x)在概率密度函数p(x)下的期望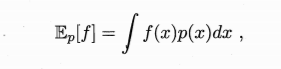
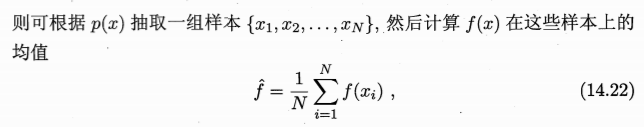 以此来近似目标期望E[f]。
以此来近似目标期望E[f]。概率图模型中最常用的采样技术是马尔可夫链蒙特卡罗(Markov ChainMonte Carlo,简称MCMC)方法。
给定连续变量x∈X的概率密度函数p(x),x在区间A中的概率可计算为: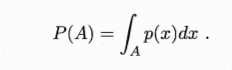
若有函数f:X→R,则可计算f(x)的期望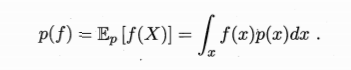
计算方法:MCMC先构造出服从p分布的独立同分布随机变量X1,2….. xN,再得到上式的无偏估计
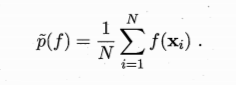
MCMC方法的关键:通过构造“平稳分布为p的马尔可夫链”来产生样本:若马尔可夫链运行时间足够长(即收敛到平稳状态),则此时产出的样本x近似服从于分布p。
如何判断马尔可夫链到达平稳状态呢?
假定平稳马尔可夫链T的状态转移概率(即从状态x转移到状态x’的概率)为T(x’ |x),t时刻状态的分布为p(x*),则若在某个时刻马尔可夫链满足平稳条件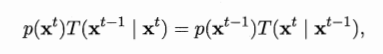
则p(x)是该马尔可夫链的平稳分布,且马尔可夫链在满足该条件时已收敛到平稳状态。MCMC方法:先设法构造一条马尔可夫链,使其收敛至平稳分布恰为待估计参数的后验分布,然后通过这条马尔可夫链来产生符合后验分布的样本,并基于这些样本来进行估计。
Metropolis Hastings (简称MH)算法(MCMC的重要代表):它基于“拒绝采样”(reject sampling)来逼近平稳分布p。
 为达到平稳状态,只需要将接受率设置为:
为达到平稳状态,只需要将接受率设置为: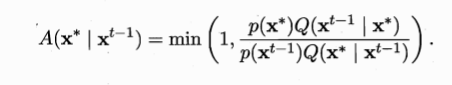
吉布斯采样(Gibbs sampling):有时被视为MH算法的特例,它也使用马尔可夫链获取样本,而该马尔可夫链的平稳分布也是采样的目标分布p(x)。
采样步骤:
(1)随机或以某个次序选取某变量xi;
(2) 根据x中除xi外的变量的现有取值,计算条件概率p(xi | x),其中
xq= {x1,W2…,Xi -1,Ti+1,…,xN} ;
(3)根据p(xi I xq)对变量xi采样,用采样值代替原值。


