感知机:好消息,对于复杂的函数,感知机也隐含着能够表示它的可能性。即便是计算机进行的复杂处理,感知机(理论上)也可以将其表示出来。坏消息,设定权重的工作,即确定合适的、能符合预期的输入与输出的权重,现在还是由人工进行的。
神经网络:为了解决感知机的坏消息。神经网络的一个重要性质是它可以自动地从数据中学习到合适的权重参数。
1 从感知机到神经网络
1.1 神经网络的例子:

图中的网络一共由 3层神经元构成,但实质上只有 2层神经元有权重,因此将其称为“2层网络”。
1.2 感知机
未表示偏置: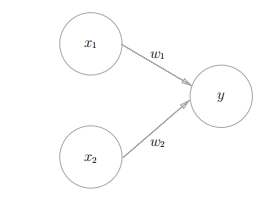
感知机数学式(式1):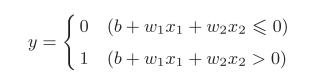
b:偏置,用于控制神经元被激活的容易程度;
w1和w2:各个信号的权重,用于控制各个信号的重要性。
改写(式2):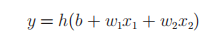
(式3):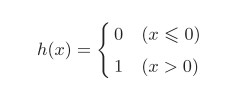
明确表示偏置: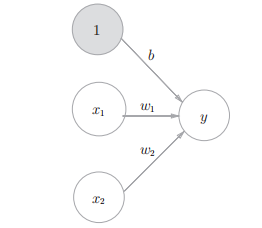
2 激活函数
激活函数:刚刚的h(x)函数会将输入信号的总和转换为输出信号,这种函数一般称为激活函数。
激活函数的作用:决定如何来激活输入信号的总和。
将式2再改写:
计算加权输入信号和偏置的总和,记为a(式4):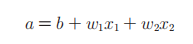
用h()函数将a转换为输出y(式5):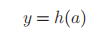
明确显示激活函数的计算过程:

“ 神经元=节点”,这里我们称a为y的节点。
激活函数的计算过程:
激活函数是连接感知机和神经网络的桥梁。
感知机可分:
1) 朴素感知机:指单层网络,指的是激活函数使用了阶跃函数的模型。
2)多层感知机:指神经网络,即使用sigmoid函数等平滑的激活函数的多层网络。
2.1 阶跃函数
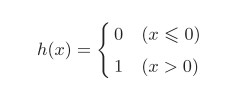
h(x)表示的激活函数以阈值为界,一旦输入超过了阈值,接切换输出,这样的函数称为“阶跃函数”。感知机中使用了阶跃函数作为激活函数。
2.2 sigmoid函数
(式6):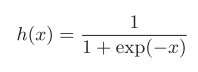
函数就是给定某个输入后,会返回某个输出的转换器。
神经网络中用sigmoid函数作为激活函数,进行信号的转换,转换后的信号被传送给下一个神经元。
感知机和神经网络的主要区别就在于这个激活函数。
2.3 sigmoid函数和阶跃函数的比较
不同:
1)平滑性:sigmoid函数是一条平滑的曲线,输出随着输入发生连续性的变化。而阶跃函数以0为界,输出发
生急剧性的变化。
2)于阶跃函数只能返回0或1,sigmoid函数可以返回0.731 …、0.880 …等实数。也就是说,感知机中神经元之间流动的是0或1的二元信号,而神经网络中流动的是连续的实数值信号。
相同:
1)它们具有相似的形状。
2)两者的结构均是“输入小时,输出接近0(为0);随着输入增大,输出向1靠近(变成1)”
当输入信号为重要信息时,
阶跃函数和sigmoid函数都会输出较大的值;当输入信号为不重要的信息时,
两者都输出较小的值。
3),不管输入信号有多小,或者有多
大,输出信号的值都在0到1之间。
2.4 非线性函数
- 阶跃函数和sigmoid函数均为非线性函数。
- 线性函数: 函数本来是输入某个值后会返回一个值的转换器。向这个转换器输入某个值后,输出值是输入值的常数倍的函数称为线性函数(用数学式表示为h(x) = cx。c为常数)。因此,线性函数是一条笔直的直线。
- 非线性函数:不像线性函数那样呈现出一条直线的函数。
- 神经网络的激活函数必须使用非线性函数。数不能使用线性函数,因为使用线性函数的话,加深神经网络的层数就没有意义了。
- 线性函数的问题在于,不管如何加深层数,总是存在与之等效的“无隐藏层的神经网络”。
eg:把线性函数 h(x) = cx 作为激活函数,把y(x) = h(h(h(x)))的运算对应3层神经网络。这个运算会进行y(x) = c × c × c × x的乘法运算,但是同样的处理可以由y(x) = ax(注意,a = c 3)这一次乘法运算(即没有隐藏层的神经网络)来表示。
2.5 ReLU函数
ReLU函数在输入大于0时,直接输出该值;在输入小于等于0时,输出0。
ReLU函数(式7):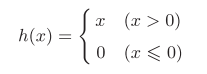

3 多维数组的运算
多维数组就是“数字的集合”,数字排成一列的集合、排成长方形的集合、排成三维状或者(更加一般化的)N维状的集合都称为多维数组。
神经网络的内积
省略了偏置和激活函数,只有权重的神经网络:
4 3层神经网络的实现

4.1 权重的符号:

4.2 各层间信号传递的实现
从输入层到第1层的第1个神经元的信号传递过程:
图中增加了表示偏置的神经元“1”。注意,偏置的右下角的索引号只有一个。这是因为前一层的偏置神经元(神经元“1”)只有一个 。
用数学式表示(式8):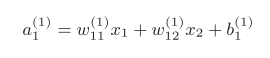
用矩阵乘法表示(式9):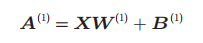
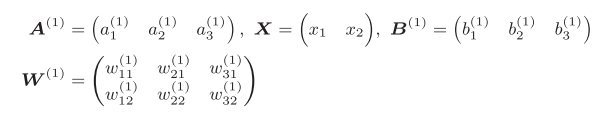
从输入层到第1层的信号传递:
隐藏层的加权和(加权信号和偏置的总和)用a表示,被激活函数转换后的信号用z表示。h()表示激活函数(这里使用的是sigmoid函数)。
第1层到第2层的信号传递:
第1层的输出(Z1)变成了第2层的输入
从第2层到输出层的信号传递:
输出层所用的激活函数,要根据求解问题的性质决定。一般地,回归问题可以使用恒等函数,二元分类问题可以使用 sigmoid函数,多元分类问题可以使用softmax函数。5 输出层的设计
一般而言,回归问题用恒等函数,分类问题用softmax函数。
机器学习的问题大致可以分为分类问题和回归问题。
分类问题:是数据属于哪一个类别的问题。
比如,区分图像中的人是男性还是女性。
回归问题:是根据某个输入预测一个(连续的)数值的问题。
比如,根据一个人的图像预测这个人的体重。
5.1 恒等函数和softmax函数
恒等函数:会将输入按原样输出,对于输入的信息,不加以任何改动地直接输出。
恒等函数进行的转换处理可以用一根箭头来表示。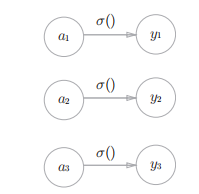
softmax函数(式10):
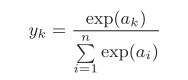
输出通过箭头与所有的输入信号相连。输出层的各个神经元都受到所有输入信号的影响。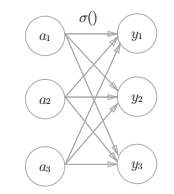
5.2 实现softmax函数时的注意事项
- softmax函数在计算机运算时有一定缺陷,可能会产生”溢出问题“。指数运算值会很大,在超大值之间进行除法运算,结果会出现”不确定性“情况。
- 计算机处理“数”时,数值必须在 4字节或 8字节的有限数据宽度内。可以表示的数值范围是有限的。因此,会出现超大值无法表示的问题。这个问题称为溢出。
- softmax函数的改进(式11):

这里的C‘可以使用任何值,但是为了防止溢出,一般会使用输入信号中的最大值。
5.3 softmax函数的特征
- softmax函数的输出是0.0到1.0之间的实数。并且,softmax函数的输出值的总和是1(重要性质)。
- 有了这个性质,我们把softmax函数的输出解释为“概率”。
- 一般而言,神经网络只把输出值最大的神经元所对应的类别作为识别结果。
并且,即便使用softmax函数,输出值最大的神经元的位置也不会变。因此,神经网络在进行分类时,输出层的softmax函数可以省略。在实际的问题中,由于指数函数的运算需要一定的计算机运算量,因此输出层的softmax函数一般会被省略。 - 求解机器学习问题的步骤可以分为“学习” 和“推理”两个阶段。
首先,在学习阶段进行模型的学习(这里的“学习”是指使用训练数据、自动调整参数的过程),然后,在推理阶段,用学到的模型对未知的数据进行推理(分类)。如前所述,推理阶段一般会省略输出层的 softmax函数。在输出层使用 softmax函数是因为它和神经网络的学习有关系。
5.4 输出层的神经元数量
输出层的神经元数量需要根据待解决的问题来决定。
分类问题:输出层的神经元数量一般设定为类别的数量
小结
本章介绍了神经网络的前向传播。
• 神经网络中的激活函数使用平滑变化的sigmoid函数或ReLU函数。
• 通过巧妙地使用NumPy多维数组,可以高效地实现神经网络。
• 机器学习的问题大体上可以分为回归问题和分类问题。
• 关于输出层的激活函数,回归问题中一般用恒等函数,分类问题中一般用softmax函数。
• 分类问题中,输出层的神经元的数量设置为要分类的类别数。
• 输入数据的集合称为批。通过以批为单位进行推理处理,能够实现高速的运算。
